Centrality Explained
What is this?
This is an explanation of how we rank members of the science and research network on Bluesky according to how influential they are.
In network analysis for social networks, the concept of centrality is typically used in an attempt to quantify the influential capacity of actors. There are many competing ways to calculate centrality; the one we use is called betweenness centrality.
The basic idea
Betweenness centrality is basically a count of how often a node (in this context an actor on Bluesky) is on the shortest path between two other nodes. The idea is, that this expresses the potential for passing along information in a network.
Betweenness centrality is an alternative to perhaps the most obvious metric: The number of connections a given actor has, sometimes called degree centrality.
Let’s look at few toy examples to develop an intuition for what this means.
Toy examples
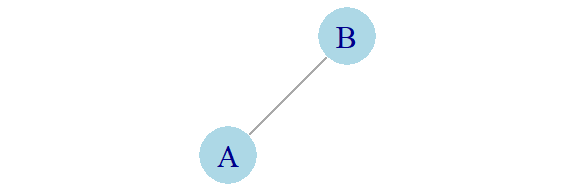
The simplest possible network has just two actors with a single connection. (The term actor is used for users on Bluesky; in network or graph theory the term node, or vertex is often used. The connection is called an edge.)
Such a network is trivially simple:
Here, each actor, A and B, clearly are in equal positions. Each has exactly one connection; we don’t really need a calculation, but let’s do one anyway. Here’s the number of connections (or the degree centrality):
A B
1 1 Since A and B are the only two actors none of them are on the shortest path between any other actors, the betweenness centrality is zero:
A B
0 0 This changes if we create a slightly less trivial network with three actors, A, B, and C:
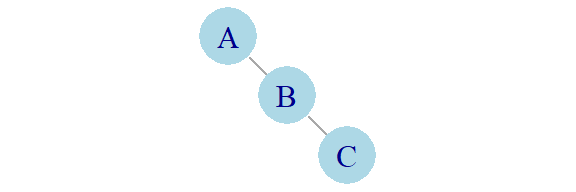
B is now clearly in a more central position than the other two actors, having two connections rather than one:
A B C
1 2 1 And also a higher betweenness centrality from being on the shortest path between the other two:
A B C
0 1 0 You can think of this as B “controlling” the flow of information from A to C.
In the simple example B wins out on centrality whether measured by number of connections or by betweenness centrality. But it doesn’t have to be like that; a bit more complicated network might look like this:
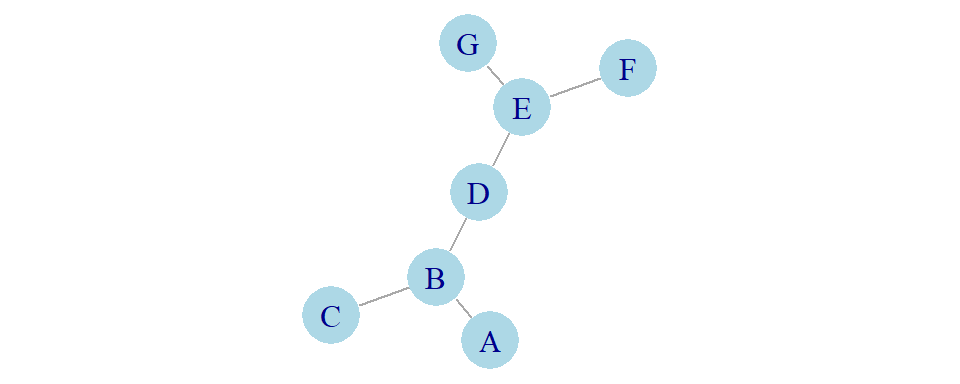
Here, B and E have the most connections, 3 each:
A B C D E F G
1 3 1 2 3 1 1 But in terms of betweenness centrality, D is now equal to B and E, since all three are on the shortest path between 9 pairs of actors:
A B C D E F G
0 9 0 9 9 0 0 It works out like this: D connects A, B, C on one side, with F, E, G on the other side, for a total of 9 possible pairs.
B connects A, C on one side, with D, E, F, G on the other (8 pairs) while also connecting A and C (1 additional pair). E is in an identical position to B, so is also on the shortest path between 9 pairs.
Real example
For a slightly bigger, real-life network, this is the friendships between 34 members of a karate club. 1

Visually it appears that members 1, 33 and 34 are particularly important members in this network. However, even in a relatively small example like this, we can no longer easily spot the number of connections, much less the betweenness centrality, so the computations are helpful.
We can plot the two centrality measures from that network in a scatter plot:

There is a rough relationship between number of connections (degree centrality) and betweenness centrality – you need some connections to have good connections – but it is not the same thing.
For example, while member number 34 has the most friendships (same as most connections, and highest degree centrality) member number 1 has the highest betweenness centrality: She may be the one that is best at bringing different people together, and the best transmitter of information, since she is on the shortest path of most pairs of members.
Science-research network
Finally, let’s do the same plot for our actual network of scientists and researchers on Bluesky. Currently, we have a total of 39030 members, so we get a dense swarm of dots. Also, the range of values spans many orders of magnitudes, so we use logarithmic axes.
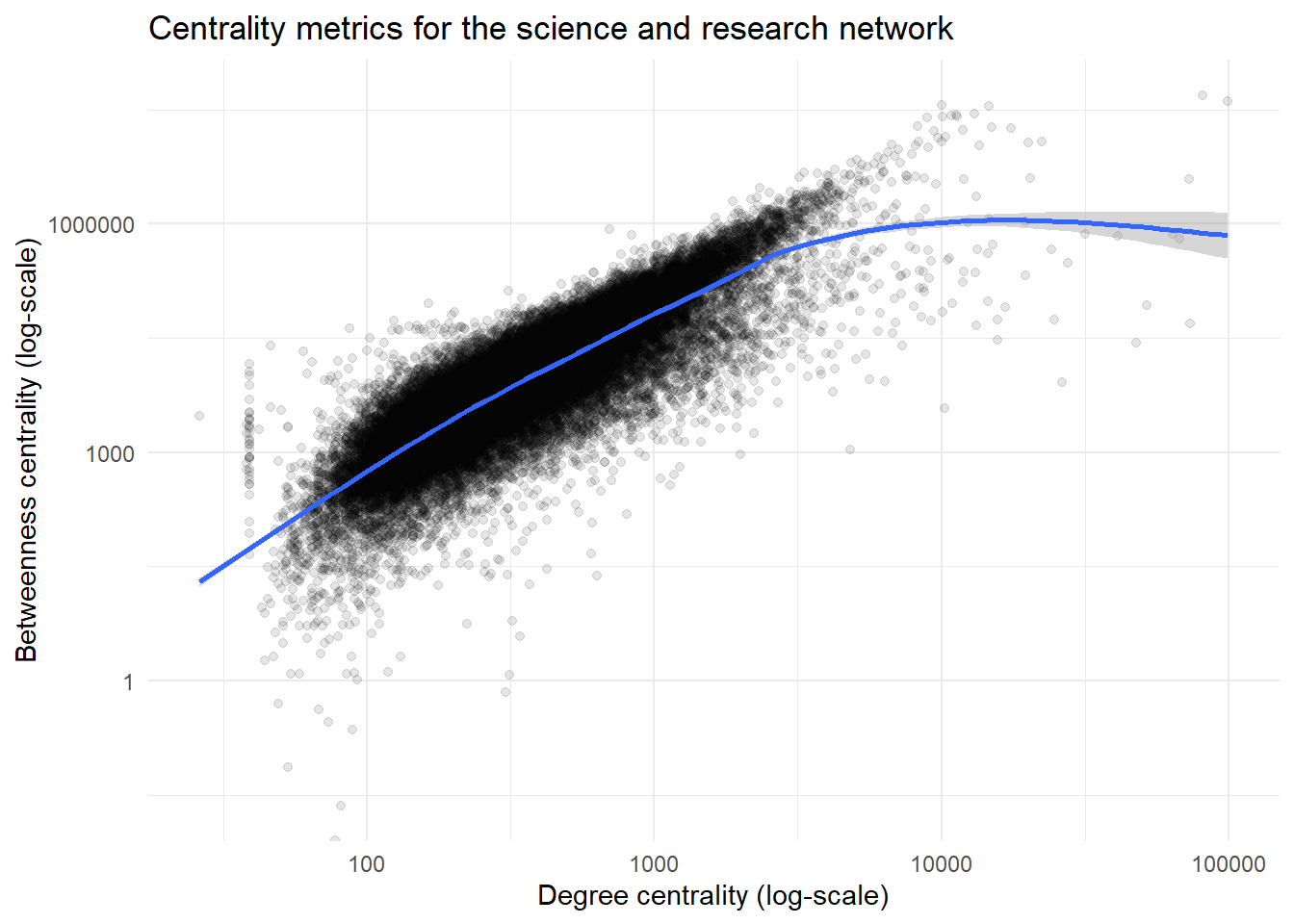
Basically the same impression as in the karate club-network: The two metrics are clearly correlated, but they are not the same thing. The curve seems to level off – the few actors with extremely many connections does not quite have the same extreme betweenness centrality.
Out of curiosity, let’s split the plot by the communities we detected. Community detection is basically smaller subsets of the network with a particular high density of connections. (Could be the topic for another note.) The communities are labeled by the three most frequent words from the profile description in each community. (We use weighted frequencies, the so-called and not so easy to remember “term frequency–inverse document frequency”).
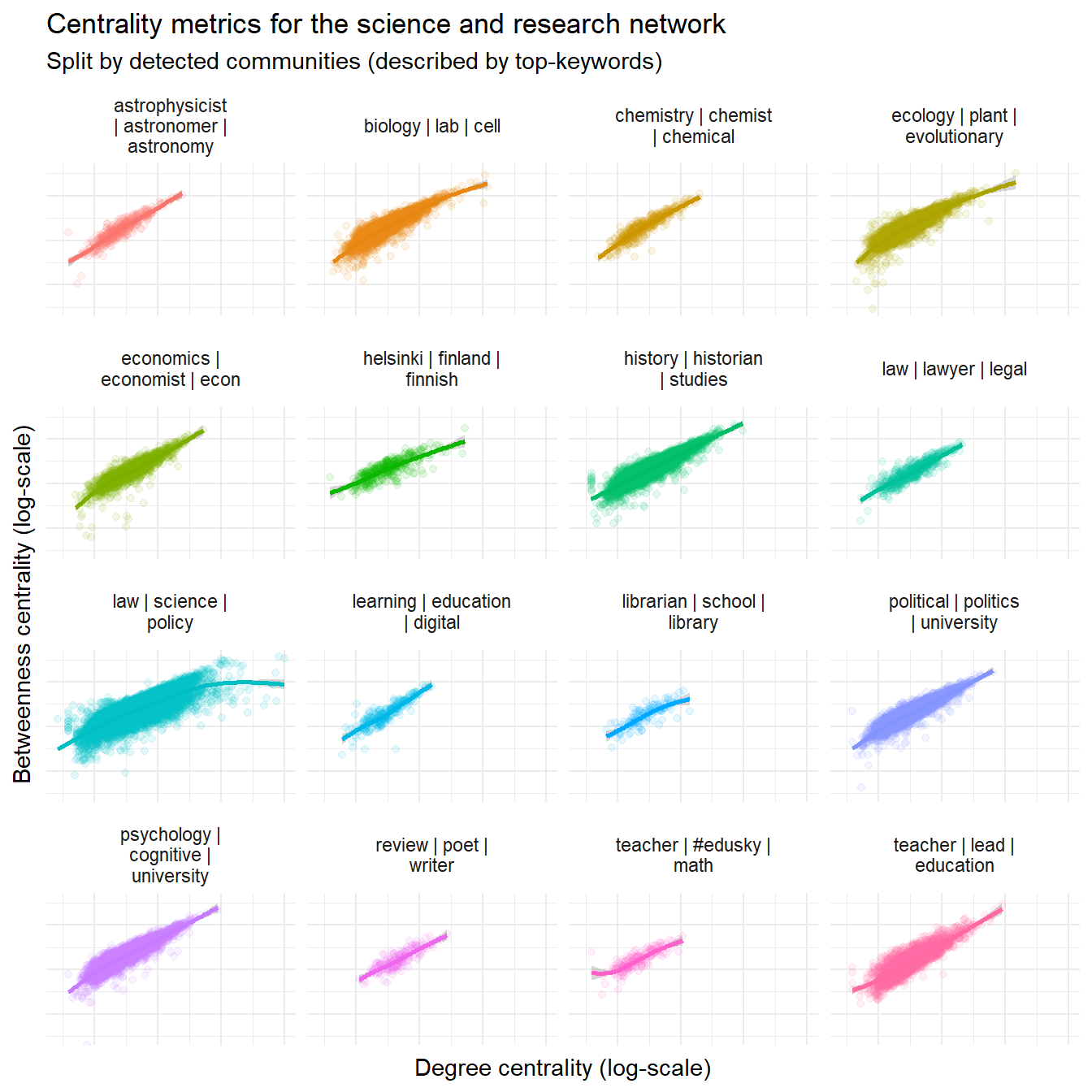
Same general correlation seems to hold for all of our sub-networks or communities, so it seems likely this is a general property of betweenness centrality: It’s related to degree centrality, but not the same. You can think of betweenness centrality as a qualification of the more naive metric of just counting connections.