| Regular | Gammon | Backgammon | Sum | |
|---|---|---|---|---|
| Player wins | 37 | 12.5 | 0.5 | 50 |
| Opponent wins | 37 | 12.5 | 0.5 | 50 |
| Sum | 74 | 25.0 | 1.0 | 100 |
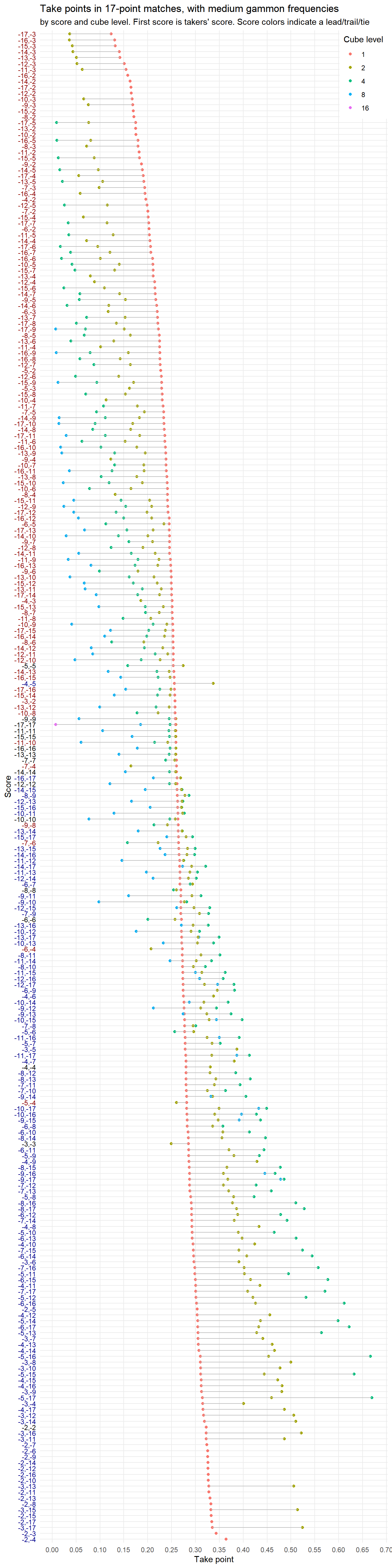
Exploring take points
Why this?
What is the lowest take point you can possibly have, with reasonable gammon frequencies? Not surprisingly, this happens when you’re trailing 17-away, 17-away, the opponent holds a 16-cube and double to 32. If you pass, you have about 1 percentage chance of winning, so if you got that many winning chances, you can take.
But what about all the other take points; which ones are the most extreme?
A big plot
These are some assumed outcome probabilities, similar to the opening position:
Using those gammon and backgammon frequencies, here’s a take point plot, for all possible scores and cube-values in a 17-point match. It’s fun to explore and learn. Can you find that one purple 16-cube mentioned in the beginning?